SECTION –A
Q1. Find the
missing number in the series: 2, 4, 5, 15, 17, 68, 71,
355, 359,
____________.
Solution. The
series is moving as
2 × 2 = 4
5 ×3 = 15
17 × 4 = 68
71 × 5 = 355
359 × 6 = 2154
Solution. 4 =
2^2, 25 = 5^2, 9 = 3^2, 81 = 9^2
270 = 2 × 5 × 3 × 9
Similarly,
2 × 8 × 9 × 6 = 844
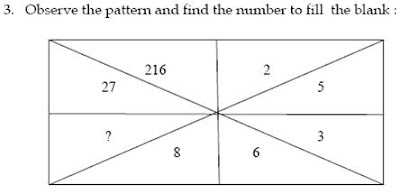
Solution. The
pattern follows as the opposite pair of numbers and their respective cubes. Thus, 5^3 = 125.
Q4. If
K = 11 and KAMAL = 38, then PRIZE = __________.
Solution. K =
11 represents the alphabet number starting from A = 1, B = 2, C = 3... K =
11... Z = 26.
Therefore, KAMAL = 11 + 1 + 13 + 1 + 12 = 38.
Similarly, PRIZE = 16 + 18 + 9 + 26 + 5 = 74.
5. What is the angle between the minute hand
and the hour hand of a clock at 15 minutes past 7?
Solution. Angle
formed between hour and minute hand @ 7 = 7 × 30° = 210°
Angle formed by minute hand in next 15 minutes = 15 × 6° =
90°
Angle formed by hour hand in next 15 minutes = 15 × 1/2° =
7(1/2)°
Total angle = 210° - {90° - 7(1/2)°} = 127(1/2)°
6. If MACHINE is coded as 197914152011, how
will you code DANGER?
Solution. The
coding follows as
MACHINE = 13 1 3
8 9 14 5
(as per their respective position in English alphabets)
Now, look at the coding given, each position is increased
by 6.
Therefore, DANGER = 4
1 14 7
5 18
Now, increase their positions by 6.
DANGER = (4 + 6) (1 + 6) (14 + 6) (7 + 6) (5 + 6) (18 + 6)
Therefore, DANGER = 10
7 20 13
11 24
Solution. The
pattern follows as
16 = 3 × 5 + 1
81 = 16 × 5 + 1
406 = 81 × 5 + 1
Next term = 406 × 5 + 1 = 2031
8. A, B, C, D, E, F, G and H are the family
members. B is the sister of G and G is the brother of C. E is the wife of A,
whose father is H. D is the husband of B and F is the son of G. A is the father
of B. How ‘F’ is related to ‘E’?
Solution. . F
is the grandson of E.
Solution. New
equation after interchanging the symbols would look like as
40 ÷ 20 + 10 x 2 – 14 = 40 × 20 ÷ 10 - 2 + 14
= 40 × 2 - 2 + 14 = 80 + 12 = 92
10. Five poles are standing in a row. M is on
the left of N, O is on the right of P which is on the right of N. If L is on
the left of M, which pole is in the centre?
Solution. The
correct arrangment would be
L M N P O
Therefore, N is standing at the centre.
SECTION - B
11. Ankit goes straight 6 km eastwards, then
turns right and goes straight 2 km and turns right again and goes straight 8
km. In which direction is he from the starting point?
Solution. South-west
Solution. 5^(a
+ b) = 5^(c - d)
As the bases are same, hence, the powers will be equal.
a + b = c - d
d = (c - a - b)
13. If the perimeter of a semicircular
protractor is 36cm, its diameter is :
Solution. Perimeter
of a semi-circular protractor = 2r + pie × radius
36 = 2r + 22r/7
36 = 36r/7
r = 7 cm
Therefore, diameter = 2 × 7 = 14 cm
14. A purchased 4 chairs and 3 tables for Rs.
1650. B purchased 3 chairs and 2 tables for Rs. 1150. The cost per chair is :
Solution. Let
the price of a chair and a table be Rs. c and Rs. t respectively.
4c + 3t = 1650 ... (i)
3c + 2t = 1150 ... (ii)
Solving (i) & (ii), we get
t = 350 and c = 150
15. If the height of a cone is halved and its
radius is doubled, then its volume is increased by :
Solution. Initial
volume of a cone = 1/3 × 22/7 × r^2 × h
New dimensions,
radius = 2r
height = h/2
New volume of the cone = 1/3 × 22/7 × (2r)^2 × (h/2) = 2/3
× 22/7 × r^2 × h
Change in volume = 2/3 × 22/7 × r^2 × h - 1/3 × 22/7 × r^2
× h = 1/3 × 22/7 × r^2 × h
Therefore, a change of 100%.
16. An equilateral triangle is formed on a
diagonal of a square of side ‘a’cm. The area of the triangle is :
Solution. Side
of square = a cm
diagonal of the square = aSqrt (2) cm
side of equilateral triangle = diagonal of the square = a
sqrt (2) cm
Area of equilateral triangle = sqrt (3)/4 × (side)^2
= sqrt (3)/4 × {a sqrt (2)}^2 = Sqrt (3)/4 × a^2 square cm
Solution. USing
equality we can say that both, a & b are positive but less than 1.
I. a is less than b which
implies (a - b) is negative. Hence, TRUE.
II. a × b will be positive which when divides 1 will
result in positive value. Hence, TRUE.
III. (a - b) is negative and ab is positive. Thus, when a
negative value is divided by a positive value will always result in negative
qunatity. Hence, FALSE.
Solution. 110°
Draw the appropriate figure and mark the given dimensions
accordingly. Use the theorem for angles formed by a transversal on parallel
lines
19. A triangle and a trapezium are equal in
area. They also have the same altitudes. If the base of the triangle is 36 cm,
the mean of the parallel sides of the trapezium is :
Solution. AS it is
given that there areas are equal
½ × 36 × altitude = ½ × (Sum of parallel sides) × altitude
Þ
Sum of the parallel sides = 36
Þ
Mean of the parallel sides = 36 ÷ 2 = 18 cm
20. The maximum number of points of
intersection of 8 lines is:
Solution. Two
straight lines can intersct atmost at 1 point.
Three straight lines can intersect atmost at 1 + 2 points.
Four straight lines can intersect atmost at 1 + 2 + 3
points.
Similarly, and so on
We can generalize this result by the formula
Þ n(n – 1)/2 where ‘n’ is the number of lines.
Here, for n = 8,
Maximum points of intersection of 8 straight lines = 8 × 7 ÷
2 = 28
Solution. 50°
22. The minute hand of a wall clock is of the
length 10.5cm. The area covered by it in 1 hour is :
Solution. In 1
hour, the hand of the clock will swap the entire 360°.
Area covered = pr2 = 346.5 cm2
23. The unit digit in (727 –
314
) is :
Solution. These
type of questions are asked in previous years. I have explained this type in
detail. Kindly refer to it. If there is any problem, then revert back.
24. When n is divided by
4, the remainder is 3. What is the remainder when 2n is
divided by 4?
Solution. Using
division algorithm,
Dividend = Divisor × Quotient + Remainder
N = 4x + 3
2(n) = 2(4x + 3) = 8x + 6
2n = 8x + 6 = {(8x + 4) + 2} = {4(2x + 1) + 2}
Now, 4( 2x + 1) is divided by 4 and 2 is left as remainder.
Solution. 1/a +
1/b = 1/c and ab = c
(a + b)/ab = 1/c
(a + b)/c = 1/c
(a + b) = 1
Average of a and b = (a + b)/2 = ½
Option (c)
26. 9 men visited a hotel, 8 of them spent
Rs.4 each over their meal and the 9th spent Rs. 2
more than the average of all the nine. The total money spent by them on the
meal is :
Solution. Let the
average money spent by 9 men be Rs. x
Total money spent by 8 of them = Rs. 4 × 8 = Rs. 32
Money spent by 9th men = Rs. (x + 2)
Total money spent by 9 men = Rs. {(x + 2) + 32}
Average money spent by 9 men = {(x + 2) + 32}/9
x = {(x + 2) + 32}/9
On solving, we get
x = 4.25
Total money spent by 9 men = 4.25 + 2 + 32 = Rs. 38.25
Option (a)
27. Of the three numbers, the first is twice
the second and is half the third. If the average of three numbers is 56 , the
three numbers in order are :
Solution. Let the
first number x
Second number = x/2
Third number = 2x
Sum of three numbers = x + x/2 + 2x = 7x/2
Average of three numbers = 56
(7x/2) ÷ 3 = 56
On solving, we get
X = 48
Therefore, the numbers are 48, 24, 96
NOTE: The
question can be solved much more easily by checking the options
Option (a)
28. The circumradius of a triangle whose
sides are 6cm, 8 cm and 10 cm is :
 Solution. We know
that angle subtended in a semi-circle is a right angle. Thus, hypotenuse of the
triangle will become the diameter of the circle or 10 cm ÷ 2 = 5 cm
Solution. We know
that angle subtended in a semi-circle is a right angle. Thus, hypotenuse of the
triangle will become the diameter of the circle or 10 cm ÷ 2 = 5 cm
29. If a, b, c, d and
e are five consecutive odd integers , then
their mean is :
Solution. Mean =
Sum of all observations ÷ Total number of observations
Mean = (a + b + c + d + e) ÷ 5
But this is not among the given options.
Lets try substituting some random values on this statement
1, 3, 5, 7, 9 and 37, 39, 41, 43, 45
Mean for 1st set = (1+ 3+ 5+7+9) ÷ 5 = 5 or
1(First number) + 4 = 5 (Mean of given set of values)
Mean of 2nd set = (37 + 39 + 41 + 43 + 45) = 41
or 37 (First number) + 4 = 41 (Mean of given set of values)
Thus, we can conclude that the average/mean of five
consecutive odd integers is always 3rd consecutive integer or 4 more
than the 1st consecutive integer.
Section C
Solution. Let x = 0.34676767…
10x = 3.4676767…
100x = 34.676767…
100x – x = (34.676767…)
– (0.34676767…)
99x = 34.33
x = 3433/9900
Similarly, let y = 0.1333333…
10y = 1.33333…
10y – y = (1.33333…)
– (0.1333333…)
9y = 1.2
y = 12/90 = 2/15
Þ
x + y = 3433/9900 + 2/15 = 4753/9900
32. The sum of a
two digit number and the number obtained by interchanging the digits of the
number is 121. If the digits of the number differ by 5 , then find the number.
Solution. Let the 2-digit number be 10x + y.
Number obtained by interchanging the digits = 10y + x
x – y = 5 or y – x = 5 …
(1)
Þ
(10x + y) + (10y + x) = 121
Þ
x + y = 11 … (2)
Solving equation (1) & (2), we get
x = 8 or 3
y = 3 or 8
Therefore, the number is 38 or 83.
33. P and Q can do
a piece of work in 12 days. Q and R in 15 days, R and P in 20 days. In how many
days R alone can do the same work?
Solution. 1/P + 1/Q = 1/12, 1/Q
+ 1/R = 1/15, 1/R + 1/P = 1/20
Adding the above three equations we get
Þ
2{1/P + 1/Q + 1/R} = 1/12 + 1/15 + 1/20 = 1/5
Þ
1/P + 1/Q + 1/R = 1/10
Þ
In 1 day, R alone can do it in = {1/P + 1/Q + 1/R } – {1/P + 1/Q }
= 1/10 – 1/12 = 1/60
Therefore, R alone can complete the whole work in 60 days.
36. Two cylinders
of same volume have their heights in the ratio 1 : 3. Find the ratio of their
radii.
Solution. V1 = p × r12
× h1 & V2
= p
× r22 × h2
Þ
V1 ÷ V2 = {r12 ÷
r22 }×{h1 ÷ h2}
V1 = V2
Þ
{h2 ÷ h1} = {r1 ÷ r2}2
Þ
r1/r2 = √ h2 /h1 = √3 : 1
37. Find the number
of spherical bullets, each 0.6cm in diameter be made out of a rectangular solid
9cm x 11 cm x 12 cm.
Solution. Volume of solid block = n × Volume of each bullet
Where ‘n’ is
number of bullets
Þ
9 × 11 × 12 = n × 4p/3 ×
(0.3)3
Þ
n = 35 × 3 × 100 = 10500
Q38. The largest sphere is cut off from a cube of diagonal 5 cm. Find the volume of the sphere.
Solution. Largest
sphere implies that the sphere would be fitted exactly into the cube.
Þ
Diagonal of sphere = Length of the edge of cube
Þ
Diagonal of cube = side√3
Þ
Side of the cube = 5 cm
Largest sphere = 4p/3 × (5)3 = 500p/3
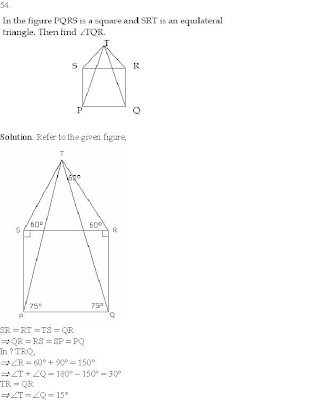
Solution. From
the given figure
b = c and 3a = (a + 2b)
b = c and a = b
Þ
a = b = c
3a + c = 180°
4c = 180°
c = 45°
40. A cylindrical vessel 60cm in diameter
is partially filled with water. A sphere 60cm in diameter is gently dropped
into the vessel. To what height will water rise in the cylinder?
Solution. Due to
the sphere the volume of water in vessel will increase.
Volume of sphere = p × 30 × 30 × h
Þ
h = 4/3 × 30 = 40 cm
41. If I drive at a
speed of 24 kmph, I reach school 5 minutes late and if I drive at 30kmph , I
reach 4 minutes too soon. Find the distance of the school from my residence.
Solution. Let the distance from the residence to school be d km and usual time to reach be t hr.
Þ
d = 24 × {t + 5/60} … (1)
and d = 30 × {t – 4/60} … (2)
Solving equation (1) and (2), we get
Þ
24 × {t + 5/60} = 30 × {t – 4/60}
Þ
t = 1/3 + 1/3 = 2/3 hr or 40 minutes
42. A chord of a
circle is 12cm in length and its distance from the centre is 8cm. Find the
length of the chord of the same circle whose distance from the centre is 6cm.
Solution. Refer to the given figure
In ∆OAE,
Þ
OA2 = 82 + 62 = 100
OA = 10 cm
In ∆ODF,
Þ
DF2 = 102 – 62 = 64
DF = 8 cm
44. How many
integers are there between 100 and 1000 all of whose digits are odd?
Solution. All the numbers between 100 to 1000 will be 3-digit
numbers.
111 113 115 117 119
131 133 135 137 139
151 153 155 157 159
171 173 175 177 179
191 193 195 197 199
Total numbers starting with ‘1’ = 5 × 5 = 25
So, in the same manner there would be 25 numbers each
starting with 3, 5, 7 and 9.
Therefore, total such numbers = 5 × 25 = 125
Solution. am × an = am
+ n
Þ
am +
n = am n
Þ
m + n = mn
Þ
m (n – 2) + n (m – 2) = mn – 2m + mn – 2n
= 2mn – 2mn = 0
46. What is the
area of a circle that is inscribed in a square of area 4 sq cm? (Write the
answer in terms of π ).
Solution. Area of square = 4
Þ
Side of square = √4 = 2 cm
Side of square = Diagonal of circle
Þ
Radius of circle = 1 cm
Area of circle = pr2 = p sq
cm
Solution. x6 – ax5 + x4
– ax3 + 3x – a + 2
Þ
x5(x – a) + x3(x –
a) + 3(x – a) + 2(a + 1)
Now,
Þ
(x – a) {x5 + x3 +
3} + 2(a + 1)
If (x – a) is factor
of above expression, then the remainder left would be 0.
Þ
2(a + 1) = 0
Þ
a = –1
48. Some problem with
the question itself
49. The following
observations have been arranged in the ascending order. If the median of the
data 29, 32, 48, 50, x, x+2, 72, 78, 84 and 95 is the mean of 75,
64, 136, 25, 15, then find the value of x.
Solution. Mean = (75 + 64 + 136 + 25 + 15) ÷ 5 = 63
Arranging the given numbers in ascending order
29, 32, 48, 50, 61(x),
63(x + 2), 72, 78, 84, 95
Number of terms = 10 (even)
Median = (n/2 + 1)th
term
= 6th
term
Solution. (√3/7)
= (√21/49) = (√21)/7 » 4.58/7 = 0.65
Section D
52. A hemispherical
bowl is made of steel of 0.25cm thickness. The inner radius of the bowl is 5cm.
Find the volume of the steel used.
Solution. Outer radius = Inner radius + Thickness = 5 + 0.25 = 5.25
cm
Volume of hemi-spherical bowl = 2p/3 × {r22 –
r12}
= 2p × {(5.25)2 – (5)2} = 5.125p cc
55. Three numbers
are in the ratio 2 : 3 : 4 and the sum of their cubes is 0.334125. Find the
largest number.
Solution. Let
the numbers be 2x, 3x, 4x
respectively.
(2x)3+ (3x)3
+ (4x)3 = 0.334125
99x3 =0.334125
On solving, we get
x = 0.15
57. The compound
interest on a certain sum of money for 2 years at 5% per annum is Rs102.50.
Find the compound interest on the same sum for the same period at 4% per annum.
Solution. Let the amount
of Rs. x.
Þ (x + 102.5) = x(1 + 5/100)2
Þ (x + 102.5) = x(105/100)2
Þ (x + 102.5) = x(11025/10000)2
10000x + 1025000 =
11025x
1025x = 1025000
x = 1000
58. A train travelling with a constant
speed crosses a 96m long platform in 12 seconds and another 141 m long platform
in 15 seconds. Find the length of the train.
Solution. Let the length of the train be l m.
Þ
(96 + l)/12 = (141 + l)/15
Þ
480 + 5l = 564 + 4l
l = 84 m
60. A shopkeeper
makes a profit of 20% even after giving a discount of 10% on the advertised
price of a printer. If he makes a profit of Rs. 450, find the advertised price.
Solution. Let the
advertised price be Rs. 100.
SP after discount = 100 – 100 × 10% = Rs. 90
CP = 90/1.2 = Rs. 75
Profit = SP – CP = 90 – 75 = Rs. 15
15 = Rs. 450
1 = Rs. 450/15 = Rs. 30
100 = 30 × 100 = Rs. 3000